KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。
算法分析说明
问题:查找一个短的字符串在一个长的字符串中的位置(具体点就是:text="The boy has no girlfriend", s="has girlfriend";现在判断在text中是否包含s,如果包含返回在text中对应的下标)。KMP算法就是一种快速的解决方案。
BF算法
BF算法是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串P的第一个字符进行匹配,若相等,则继续比较S的第二个字符和P的第二个字符;若不相等,则比较S的第二个字符和P的第一个字符,依次比较下去,直到得出最后的匹配结果。时间复杂度为O(n*m)。
Java版本
public static int bfMatch(String text, String s){
int m = s.length();
int n = text.length();
if(m>n){
return -1;
}
int i=0;
while (i<n){
// if(text.substring(i).startsWith(s)){
// return i;
// }
int j = 0;
while (j<m && text.charAt(i) == s.charAt(j)){
j++;
i++;
}
if(j==m){
return i-m;
}
// 回溯
i = i-j+1;
}
return -1;
}Golang版
func bfMatch(text string, s string) int {
m, n := len(s), len(text)
if m > n {
return -1
}
i :=0
for i<n {
j :=0
// 我们这里默认没有中文字符
for j < m && text[i]==s[j] {
j++
i++
}
if j==m {
return i-m
}
// 回溯
i = i-j+1
}
return -1
}KMP算法
KMP算法是一种无回溯的算法;时间和空间复杂度都为为O(m+n)。上面的算法中我们发现其实每次不用在匹配失败后重新回到前面去,想象一下如果是人脑去匹配会如何做?
我们在匹配失败后是不会重新回到前面去的,为什么呢?因为我们知道一些已经匹配的,就不用再去弄了。
KMP算法是利用已经部分匹配这个有效信息,保持i指针不回溯,通过修改j指针,让模式串尽量地移动到有效的位置;也就是要解决当某一个字符与主串不匹配时,我们应该知道j指针要移动到哪?
我们假设重新移动的位置为k,那么要保证移动后前面的一部分是匹配的,那一定是前面长度为k的字符串和j前面的k个字符串是匹配的,这样才可以保证后面不需要重新在匹配了;下面我们举个例子来说明。
假设现在模式串匹配到下标为j的位置发现不匹配,此时目标串的下标i不变,现在移动模式串的下标到k开始重新匹配;那么需要满足如下条件:模式串(0k-1) = 模式串(j-kj-1);我们下面来画个图进行说明。
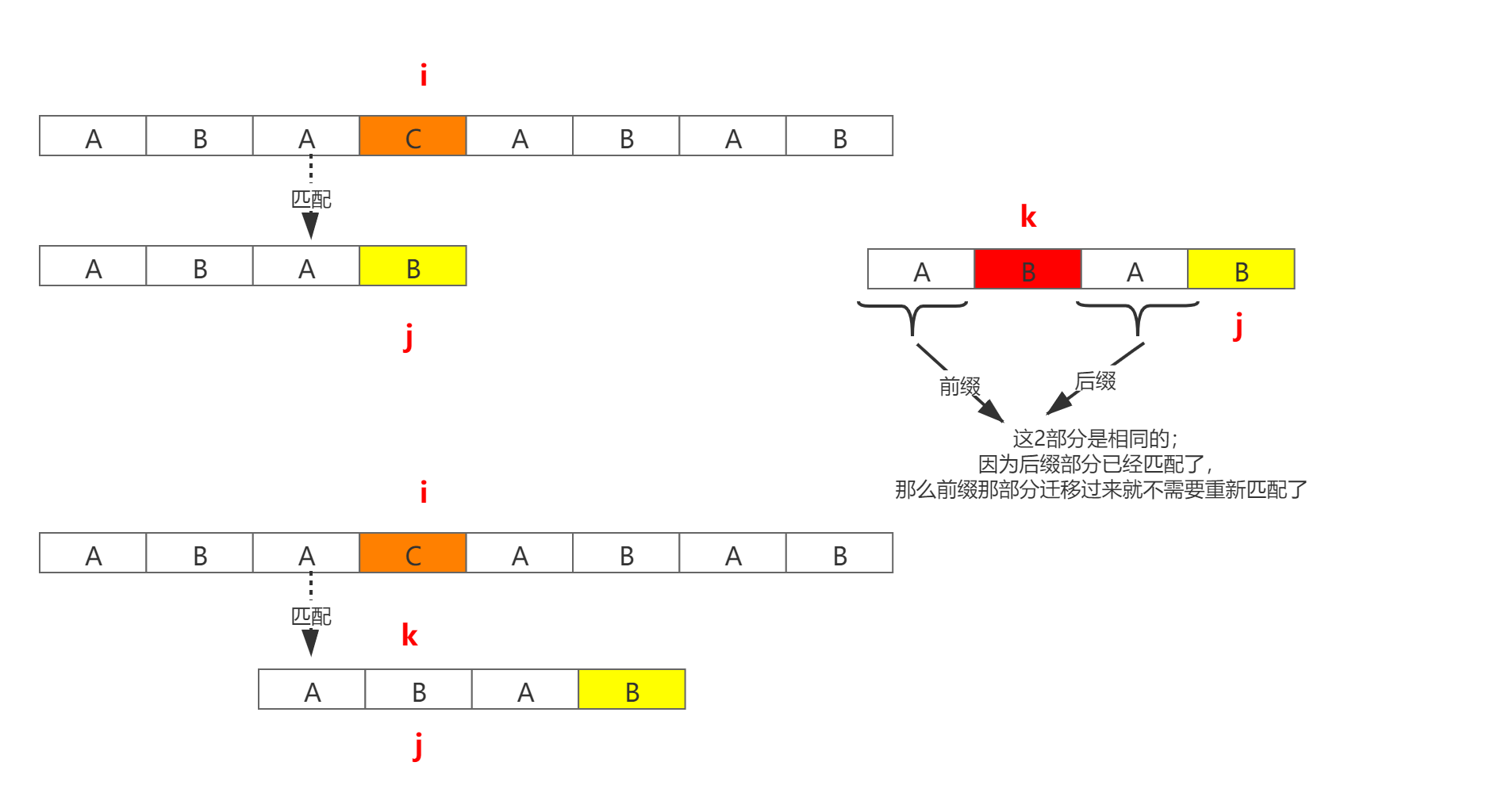
也就是说我们只动模式串,如果在i前面的存在匹配的组合,那么一定有一部分是和模式串的一部分匹配的,而k前面的那部分就是匹配的。
算法定义
- next: 为对应模式串的数组,里面保存的值就是前后缀最长的匹配数,也就是在遇到不匹配时j重新移动的开始位置。
- 设模式串为P,则next[j]=k,当且仅当满足如下条件:P[0 ~ k-1] == P[j-k ~ j-1]
- 通俗地讲: next[j]保存了以S[j]为结尾的后缀与模式串前缀的最长匹配数。
这里举个列子来说明如何计算next[j]的值。
对应下标:0 1 2 3 4 5 6 7 8 9
模式串为:a b c a b c d d e a
next: 0 0 0 0 1 2 3 0 0 0当j=5时,当前用到的字符串为abcab c; 它的后缀有:b, ab, cab, bcab, abcab;前缀有:ac, ab, abc, abca, abcab;最后的abcab是无效的,那么前后缀中匹配的最大长度是2。因为数组的下标是从0开始,因此直接使用最长匹配数正好移动位置就是已经匹配过的。
Golang版
主要是求的next的实现,我们通过下面通过2中方式来实现。
直接求解法:挨着去找每一段的前后缀最长匹配串长度;这种方式很好理解就不过多说明了。
func getNext1(p string) []int {
i, j, pLen := 0, 0, len(p)
next := make([]int, pLen)
for ; i<pLen;i++{
if i == 0 {
next[i] = -1
}else if i ==1 {
next[i] = 0
}else {
tmp := i-1
// 前后比较串的长度依次剪短,这样如果某次循环时,如果串匹配那么就是最长匹配串
for j=tmp; j>0; j--{
// 判断P[0~j] == P[tmp-j+1, tmp]
s := p[0:j]
e := p[tmp-j+1:i]
if s == e {
next[i] = j
break
}
//if compare(p, j, i, tmp-j+1) {
// next[i] = j
// break
//}
}
if j == 0 {
next[i] = 0
}
}
}
return next
}
func compare(p string, prefixEnd int, suffixEnd int, suffixStart int) bool {
prefixStart := 0
for ; prefixStart<prefixEnd && suffixStart<suffixEnd; {
if p[prefixStart] != p[suffixStart] {
return false
}
suffixStart++
prefixStart++
}
return true
}按照递推的思想求next:这种方式比较抽象,这里进行一些说明,希望可以帮助理解。 其实这种推导的方式就是优化了内层循环中找前后缀最大匹配长度的过程;我们分析上面算法的内层循环查找最大匹配串时,发现前后缀的规则(定义前缀的结束点为k,后缀的结束点为i),其中前缀的起始都是从下标0开始的,而后缀的终点都是i,如果不匹配前后缀都会减1。下面我们分情况来讨论:
对于每次内层循环都在第一次就匹配成功的情况:那么本次匹配和上一次的匹配的区别是啥,区别就是前后缀就只多了一个字符,我们只需要判断这一个字符是否相同就可以判断本次是否匹配了,即P[i] = P[K];同时本次的最大匹配长度就是k+1; 因为我们的后缀是包含了当前i这个位置的字符的,所有求得就是i+1处的移动位置,因此
next[i+1] = k+1。对于内层循环中需要进行多次才能判断是否有匹配的情况:这个时候我们换个角度来看这个过程,在这个过程中如果匹配失败,前后缀长度会减1之后再次比较;我们把这个过程抽象一下是否就是在P[0-i]中找P[0-k],而此时正好匹配到i和k这个位置,现在发现不匹配了,因此需要移动位置重新开始匹配,嘿 这不就是kmp算法中在匹配过程中遇到不匹配时找k的移动位置的情况吗;因为此时 i>k,那么next[k]的最长匹配串已经求出来了,也就是说现在已经知道k应该重新开始的位置了即
k=next[k]。
func getNext(p string) []int {
i, k, sLen := 0, -1, len(p)
next := make([]int, sLen)
next[0] = -1
for i < sLen {
if k == -1 || p[i] == p[k] { // P[i]==P[k]
k++
i++
if i < sLen {
next[i] = k
}
}else { // P[i]!=P[k]
k = next[k]
}
}
return next
}kmp比较算法:这里只需要遍历目标串text即可,匹配失败时直接从next中获取模式串的下标变化情况。时间复杂度为O(n)
func kmp(text string, p string, next []int) int {
i, j, tLen, pLen := 0, 0, len(text), len(p)
for i < tLen {
if j == -1 || text[i] == p[j] {
i++
j++
}else {
// 匹配失败,移动模式串的位置
j = next[j]
}
if j == pLen {
// 匹配成功
return i-pLen
}
}
return -1
}Java版
直接求解法
public int[] getNext(String p){
int len = p.length();
int j = 0;
int[] next = new int[len];
for (int i=0; i<len; i++){
if(i==0){
next[i] = -1;
}else if(i==1){
next[i] = 0;
}else {
int tmp = i-1;
for (j=tmp; j>0; j--){
if (p.substring(tmp-j+1, i).startsWith(p.substring(0, j))) {
next[i] = j;
break;
}
}
if (j == 0){
next[i] = 0;
}
}
}
return next;
}按照递推的思想求next
public int[] getNext(String p){
int i=0;
int k=-1;
int[] next = new int[p.length()];
next[0] = -1;
while (i<p.length()) {
if(k==-1 || p.charAt(i)==p.charAt(k)){
k++;
i++;
if(i<p.length()){
next[i] = k;
}
}else {
k = next[k];
}
}
return next;
}kmp比较算法
public int kmp(String text, String p){
// 求next
int[] next = getNext(p);
int k = 0;
int i = 0;
while (i<text.length()){
if ( k==-1 || text.charAt(i)==p.charAt(k)){
i++;
k++;
}else {
k = next[k];
}
if (k==p.length()){
return i-k;
}
}
return -1;
}



